V-fold Cross Validation

The method used by DTREG to determine the optimal tree size is V-fold cross validation. Research has shown that this method is highly accurate, and it has the advantage of not requiring a separate, independent dataset for accessing the accuracy and size of the tree.

If a tree is built using a specific learning dataset, and then independent test datasets are run through the tree, the classification error rate for the test data will decrease as the tree increases in size until it reaches a minimum at some specific size. It the tree is grown beyond that point, the classification errors will either remain constant or increase. A graph showing how classification errors typically vary with tree size is shown below:

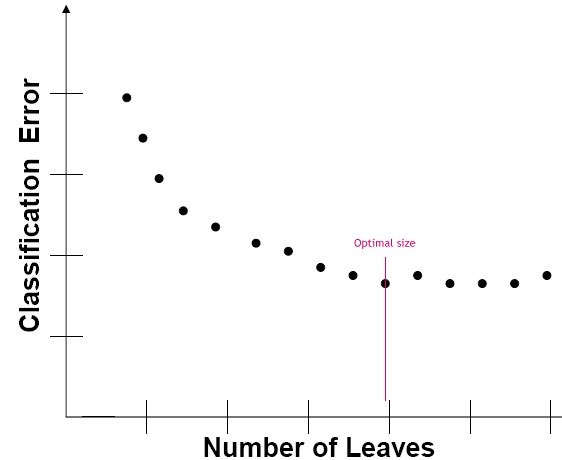
In order to perform tests to measure classification error as a function of tree size, it is necessary to have test data samples independent of the learning dataset that was used to build the tree. However, independent test data frequently is difficult or expensive to obtain, and it is undesirable to hold back data from the learning dataset to use for a separate test because that weakens the learning dataset. V-fold cross validation is a technique for performing independent tree size tests without requiring separate test datasets and without reducing the data used to build the tree.

Cross validation would seem to be paradoxical: we need independent data that was not used to build the tree to measure the generalized classification error, but we want to use all data to build the tree. Here is how cross validation avoids this paradox.

All of the rows in the learning dataset are used to build the tree. This tree is intentionally allowed to grow larger than is likely to be optimal. This is called the reference, unpruned tree. The reference tree is the best tree that fits the learning dataset.

Next, the learning dataset is partitioned into some number of groups called “folds”. The partitioning is done using stratification methods so that the distribution of categories of the target variable are approximately the same in the partitioned groups. The number of groups that the rows are partitioned into is the ‘V’ in “V-fold cross classification”. Research has shown that little is gained by using more than 10 partitions, so 10 is the recommended and default number of partitions in DTREG.

For the point of discussion, let’s assume 10 partitions are created. DTREG then collects the rows in 9 of the partitions into a new pseudo-learning dataset. A test tree is built using this pseudo-learning dataset. The quality of the test tree for fitting the full learning dataset will, in general, be inferior to the reference tree because only 90% of the data was used to build it. Since the 10% (1 out of 10 partitions) of the data that was held back from the test tree build is independent of the test tree, it can be used as an independent test sample for the test tree.

The 10% of the data that was held back when the test tree was built is run through the test tree and the classification error for that data is computed. This error rate is stored as the independent test error rate for the first test tree.

A different set of 9 partitions is now collected into a new pseudo-learning dataset. The partition being held back this time is selected so that it is different than the partition held back for the first test tree. A second test tree is built and its classification error is computed using the data that was held back when it was built.

This process is repeated 10 times, building 10 separate test trees. In each case, 90% of the data is used to build a test tree and 10% is held back for independent testing. A different 10% is held back for each test tree.

Once the 10 test trees have been built, their classification error rate as a function of tree size is averaged. This averaged error rate for a particular tree size is known as the “Cross Validation cost” (or “CV cost). The cross validation cost for each size of the test trees is computed. The tree size that produces the minimum cross validation cost is found. This size is labeled as “Minimum CV” in the tree size report DTREG generates.

The reference tree is then pruned to the number of nodes matching the size that produces the minimum cross validation cost. The pruning is done in a stepwise fashion, removing the least important nodes during each pruning cycle. The decision as to which node is the “least important” is based on the cost complexity measure as described in Classification And Regression Trees by Breiman, Friedman, Olshen and Stone.

It is important to note that the test trees built during the cross-validation process are used only to find the optimal tree size. Their structure (which may be different in each test tree) has no bearing on the structure of the reference tree which is constructed using the full learning dataset. The reference tree pruned back to the optimal size determined by cross validation is the best tree to use for scoring future datasets.

Adjusting the Optimal Tree Size

If you plot the cross-validation error cost for a tree versus tree size, the error cost will drop to a minimum point at some tree size, then it will rise as the tree size is increased beyond that point. Often, the error cost will bounce up and down in the vicinity of the minimum point, and there will be a range of tree sizes that produce approximately the same low error cost. A graph illustrating this is shown below:

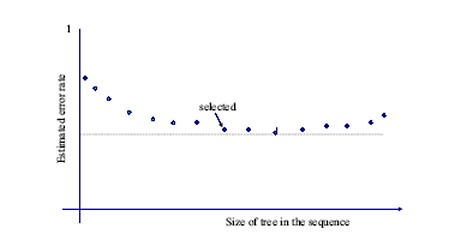
Note that the absolutely smallest misclassification cost is only slightly smaller than the misclassification cost for a tree that is several nodes smaller. Since smaller and simpler trees are preferred over larger trees that have the same predictive accuracy, you may prefer to prune back to the smaller tree if the increase in misclassification cost is minimal. The cross validation cost for each possible tree size is displayed in the Tree Size report that DTREG generates.

On the “Validation” property page for the model, DTREG provides several options for controlling the size that is used for pruning:

• Prune to the minimum cross-validated error – If you select this option, DTREG will prune the tree to the size the produces the absolutely minimum cross-validated classification error.
• Allow 1 standard error from minimum – Many researchers believe that it is acceptable to prune to a smaller tree as long as the increase in misclassification cost does not exceed one standard error of the variance in the cross validation misclassification cost. The standard error for the cross validation cost values is displayed in the Tree Size report.
• Allow this many S.E. from the minimum – Using this option, you can specify an exact number of standard errors from the minimum misclassification cost you will allow.