K-Means Clustering
Developed between 1975 and 1977 by J. A. Hartigan and M. A. Wong, K-Means clustering is one of the older predictive modeling methods. K-Means Clustering is a relatively fast modeling method, but it is also among the least accurate models that DTREG offers.
The basic idea of K-Means clustering is that clusters of items with the same target category are identified, and predictions for new data items are made by assuming they are of the same type as the nearest cluster center.
K-Means clustering is similar to two other more modern methods:
- Radial Basis Function neural networks. An RBF network also identifies the centers of clusters, but RBF networks make predictions by considering the Gaussian-weighted distance to all other cluster centers rather than just the closest one.
- Probabilistic Neural Networks Each data point is treated as a separate cluster, and a prediction is made by computed the Gaussian-weighted distance to each point.
Usually, both RBF networks and PNN networks are more accurate than K-Means clustering models. PNN networks are among the most accurate of all methods, but they become impractically slow when there are more than about 10000 rows in the training data file. K-Means clustering is faster than RBF or PNN networks, and it can handle large training files.
K-Means clustering can be used only for classification (i.e., with a categorical target variable), not for regression. The target variable may have two or more categories.
To understand K-Means clustering, consider a classification involving two target categories and two predictor variables. The following figure (Balakrishnama and Ganapathiraju) shows a plot of two categories of items. Category 1 points are marked by circles, and category 2 points are marked by asterisks. The approximate center of the category 1 point cluster is marked "C1", and the center of category 2 points is marked "C2".
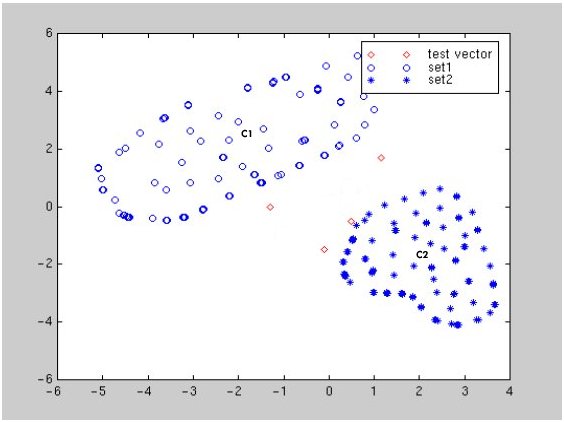
Four points with unknown categories are shown by diamonds. K-Means clustering predicts the categories for the unknown points by assigning them the category of the closest cluster center (C1 or C2).
There are two issues in creating a K-Means clustering model:
- Determine the optimal number of clusters to create.
- Determine the center of each cluster.
Given the number of clusters, the second part of the problem is determining where to place the center of each cluster. Often, points are scattered and don't fall into easily recognizable groupings. Cluster center determination is done in two steps:
- Determine starting positions for the clusters. This is performed in two steps:
- Assign the first center to a random point.
- Find the point furthest from any existing center and assign the next center to it. Repeat this until the specified number of cluster centers have been found.
- Adjust the center positions until they are optimized. DTREG does this using a modified version of the Hartigan-Wong algorithm that is much more efficient than the original algorithm.

